Perfect-Precision 2D Geometry Using Complex Integer Rings

Everybody with a STEM degree knows and (hopefully) loves complex numbers, but I bet that most people have never heard of complex integer rings. One reason could be that it appears to be a niche pure math topic with no practical applications. At least, that is what you could come to believe after skimming relevant Wikipedia articles.

The idea seems to come from a parallel universe where people discovered $\mathbb{N}$, $\mathbb{Z}$, maybe even $\mathbb{Q}$, but did not care about continuity – skipping $\mathbb{R}$. Instead, they directly tried to extend $\mathbb{Z}$ into a second dimension. This extension can be done in different ways, and each way gives us a commutative ring of complex-valued integers.

If I had stumbled into that topic without any context, I would have just moved on. However, in this post I want to convince you that complex integers are actually a pretty neat concept. In fact, I accidentally reinvented it from scratch while trying to find a solution to a rather concrete problem related to 2D geometry – the need to trace out points along polygon boundaries with perfect precision.

Update (31.01.2024):
In this repo there is an implementation of everything shown here, and more!

Update (12.01.2025):
Added and expanded explanations concerning the general mathematical properties of cyclotomic rings and the practical implementation.

Update (16.01.2025):
Here you can find the long-promised part 2!

Motivation: 2D Geometry without Floating Point Numbers

Imagine that you want to do some simple 2D geometry – working with points, line segments and polygons. Typically we do this in $\mathbb{R}^2$, the familiar Euclidean plane. Here we can measure distances and angles, express rotations, translations and much more, but there is one problem – we heavily depend on real numbers, which we typically approximate using floating point numbers. Mathematicians might be blissfully ignorant about it, but anyone who implements geometric algorithms in practice knows the pain of working with floating-point arithmetic:

• Floating point numbers can behave weird with $\pm 0$, $\pm \infty$ and NaN
• Precision is limited – very small and very large numbers are not exact
• Checking for equality is dangerous without some $\varepsilon>0$ of tolerance

Instead of $\mathbb{R}^2$ we can use $\mathbb{C}$ and pretend that the imaginary axis is our $y$ axis. This makes some things easier and more elegant. For example, there is no more need for trigonometric functions and rotation matrices, as rotations turn into multiplication with $e^{i\pi k}$.

As complex numbers are canonically represented as a pair of two real numbers, this could be considered a cosmetic change. Yet, it is the first step towards to the solution, as complex numbers are intrinsically two-dimensional. What is left to do is getting rid of the real numbers underneath, to free ourselves from the floating-point plague.

Now you could scream “But what about performance? Modern CPUs and GPUs are heavily optimized for crunching floating point numbers!”, and if that is your major concern, than probably you will not get much out of this post. If you want to develop a game or render an animation, all of this is a huge waste of your time. But if you are interested in working with polygons abstractly, e.g. in the context of tilings, and also happen to value correctness over speed in your use case, then you will agree that floating point numbers can be a major nuisance.

Discretizing The Complex Numbers

As it is widely known, each complex number can be written in polar coordinates in the form $r e^{i\pi\theta}$, with a length $r\in\mathbb{R}$ and an angle $\theta\in[-\pi, \pi]$.

While it might not be the canonical story of how complex numbers are derived, one can also imagine that the complex number field is actually generated algebraically, by starting with the length unit $1 = 1\cdot e^{i\pi\cdot 0}$, and closing it under scaling and rotations, i.e. every point of the complex plane is representable by a combination of a scaling of the length unit by $r$ (this gives you the real line), and then rotating all these points by all possible angles $\theta$.^[1] To this set of points now attach all the structure and common operations you expect to have at your disposal (such as addition and multiplication), and there you have your familiar complex number field.

Now here is a crazy idea: what if we could make both $r$ and $\theta$ integers?

Making the length discrete is simple – just restrict $r$ to $\mathbb{Z}$ and only allow scaling by integers. But what about rotations? Just like the number 1 is the smallest, atomic unit of length in the integers, let us do something similar to rotations and pick a smallest, atomic unit of rotation. Can we build a number system where we have not only “pixelated” lengths, but also rotation steps? And which angle should we pick?

Numbers With Symbolic Complex Root Dimensions

Let us start very simple and say that the smallest rotation we want to allow is 90 degrees, which is $\frac{1}{4}$ of a full turn and can be written as $e^{i \frac{\pi}{2}} = i$. If we now require that each number must be of the form $a + bi$ with $a, b \in \mathbb{Z}$ and check that operations on these numbers result only in numbers with the same property, then we have accidentally rediscovered the Gaussian integers, also written $\mathbb{Z}[i]$. Gaussian integers form a square grid in the complex plane on which you can perform most common operations (notably, excluding division – making it a commutative ring and not a field), but we are limited to rotations that are multiples of 90 degrees, making $i$ our unit of rotation.

Let us stick with Gaussian integers for a moment and massage them a little bit. The transformations might look unmotivated, but I promise that everything will fall into place soon. First, notice that each Gaussian integer is a pair of integers where each number gives us a magnitude along a dimension – one dimension is $1$ and the other is $i$. Also note that $i$ is a symbolic root, a fancy name given to $\sqrt{-1}$, and trivially, we have $1 = \sqrt{1}$. So each Gaussian integer can be written as $a\cdot \sqrt{1} + b \cdot \sqrt{-1} = (a+bi)\sqrt{1}$, and each number can be rotated by $e^{i\pi\cdot k} = i^k = (i\cdot\sqrt{1})^k$.

Rotating by only 90 degrees is quite limiting, so let’s move on to 60 degrees. A rotation by 60 degrees is $\frac{1}{6}$ of a full turn. This rotation can be written as:

$$ e^{i\frac{\pi}{3}} = \frac{1}{2} + \frac{i\sqrt{3}}{2} $$

So for 60 degree rotations we need to track terms involving $\sqrt{3}$, because this is an irrational number, and we do not want to evaluate those (remember the evil floating point numbers!). So what we do now is pretending that, just like $i$, the number $\sqrt{3}$ is a special symbolic term and we consider it to be the magnitude along another pseudo-dimension of our “60-degree-rotatable complex integers” that only intersects with the real axis in the origin (i.e. just like the imaginary axis).

Walking around the unit circle in steps of 60 degrees, you can convince yourself that all six rotations $e^{k\cdot i\frac{\pi}{3}}$ for $k\in\{0,1,2,3,4,5\}$ can be written in the form $\frac{1}{2}(a + b\cdot i\sqrt{3})$ for some $a, b \in\mathbb{Z}$. Now if you check which complex numbers can be reached by iteratively adding and multiplying only numbers that can be factored in that way, you might notice that we rediscovered the Eisenstein integers, which form a triangular grid in the complex plane.

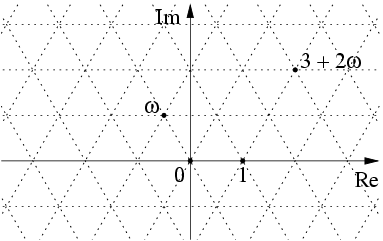
In other words, the closure of the six rotated units (i.e. the numbers corresponding to the set of unit length vectors pointing in all possible directions) under all operations in a commutative ring (such as $+$ and $\cdot$) generates the Eisenstein integers. Furthermore, these rotated units themselves are redundant, as they are generated by repeated multiplication of what we can identify as, respectively, the length unit and the rotation unit of our new number system:

$$ 1 = \frac{1}{2}(2 + 0\cdot i\sqrt{3}),\hspace{5mm} e^{i\frac{\pi}{3}} = \frac{1}{2}(1 + 1\cdot i\sqrt{3}) $$

Note that in this structure, the derived rotated units form a cyclic group that can act on any point. In that sense, the Gaussian integers essentially combine $\mathbb{Z}$ with $\mathbb{Z}_4$, whereas Eisenstein integers correspond to $\mathbb{Z}$ with $\mathbb{Z}_6$. So what we did here is substituting the continuous rotation symmetry of the unit circle with the discrete symmetry of a cyclic group. This naturally corresponds to a regular polygon in the complex plane whose vertices are located at coordinates of the different rotated units $e^{k\cdot i\frac{\pi}{3}}$.

This is pretty neat, but still of rather limited use. In the Gaussian integers we can trace out squares, rectangles or polyminoes, with the Eisenstein integers we can walk along the boundaries of hexagons, triangles, polyiamonds or polyhexes, but we can’t do both in the same number system. If we are interested in representing more general polygons, these rings are not enough – we need finer angles.

The Happy Family of Cyclotomic Integer Rings

Were we just lucky with $i$ and $\sqrt{3}$, or are there other angles from which we can derive a similar complex integer ring? Well, I will spare you the convoluted path of my personal discovery of these structures and just jump straight to the answers I found.

It turns out that what I casually called a complex integer ring is actually called cyclotomic ring, which is a cyclotomic field without the division. Essentially, these well-studied fields are based on extending $\mathbb{Q}$ into the complex plane, instead of $\mathbb{Z}$. They are called cyclo-tomic because they are based on subdivisions of the circle, perfectly matching the intuition we built earlier. So each cyclotomic ring is based on an extension of $\mathbb{Z}$ by a root of unity.

Elements of these fields are constructible, i.e. expressible by an explicit symbolic representation using simple algebraic expressions involving square roots (like the Gaussian or Eisenstein integers), only for certain parameters and are strongly connected to constructible polygons.

Definition: An angle $\frac{2\pi}{k}$ is constructible iff $k$ is a power of two, multiplied by a subset of distinct Fermat primes.

Note that currently the only known Fermat primes are $\{3, 5, 17, 257, 65537\}$ and it is conjectured that these are the only ones that exist. By $\mathbb{Z}\mathbb{Z}_r$ I will denote the ring with $\frac{1}{r}$ of a turn as the smallest rotation (in math literature you will usually see something like $\mathbb{Z}[\zeta_r]$)

Proposition: $\mathbb{Z}\mathbb{Z}_{2k}$ can be constructed iff $\frac{2\cdot\pi}{k}$ is a constructible angle.

A result of abstract algebra is that each constructible cyclotomic ring (or field) is obtained by a finite sequence of quadratic extensions of $\mathbb{Z}$ (or $\mathbb{Q}$). Cyclotomic fields were one of the foundational structures studied by and foundational for modern algebraic number theory. There are whole books written about them, but it seems to be only reasonably well known in the circles of professional mathematics. There are also larger and more complicated fields, such as the universal cyclotomic field, which contains all roots of unity, and the field of constructible numbers, is closed under square roots (both of these contain the constructible cyclotomic fields as subfields).

From the practical side of things however, we are mostly interested in what we can do with these numbers and how they can be implemented. In the following, I will explain how I came up with a representation, which might be not the way it is done in a typical CAS, but is very elementary and does not need any advanced algebraic understanding.

Explicit Representations of Cyclotomic Rings

First, remember the weird way how I wrote down the numbers in the earlier sections. The reason for this is that everything you already saw and will see here neatly fits into the same general pattern that I use for my construction.

Definition: A number $z \in \mathbb{C}$ is a symbolic complex root number if it can be written as $\frac{1}{l}\sum_{k=1}^{n} c_k\sqrt{d_k}$, where $l\in\mathbb{N}$ and for all $k$ we have $c_k \in \mathbb{Z}[i]$ and $d_k \in \mathbb{R}_+$.

Note: The coefficients $c_k \in \mathbb{Z}[i]$ can be substituted by requiring $a_k + b_k i$ with $a_k, b_k \in \mathbb{Z}$, but using Gaussian integers as first-class citizens here is not just a syntactic change, but actually immensely simplifies computation in practice.

To construct a cyclotomic ring for a fixed parameter $r$, what you need to do is:

1. find a representation of $e^{\frac{2\pi i}{r}}$ matching the definition above
2. list all non-reducible and linearly independent square root expressions that can arise due to multiplication of this unit with itself
3. figure out multiplication over vectors that have these roots as coefficients

Without any further ado, in the following table I present to you many cyclotomic rings that I was able to construct (some more are implemented in my library). The mere existence of these rings is not news, but a practical parametrization and implementation is not something I was able to find in an easily accessible and usable form anywhere (without pulling in rather heavy-weight libraries), so I hope it can be of some value. Here is the legend of the table:

• name: memorable name for the cyclotomic ring
• $r$: the smallest possible rotation is $\frac{1}{r}$ or a full turn
• $l$: scaling factor to fit into the normal form with integer coefficients
• $n$: number of distinct roots needed to represent a number in the ring
• $d_k$: list of squares of those required symbolic roots
• unit: the smallest possible rotation $e^{\frac{2\pi i}{r}}$, expressed in the normal form

The set for $r=20$, for example, is what I called the Penrose integers^[2], because they allow for the five-fold symmetry needed to draw Penrose tiles. The compass integers I named that way because you can go in all the 8 directions labelled on a compass, the clock integers I think are self-explanatory, and the digiclock integers are essentially “finer clock integers” and unite the degrees of freedom provided by the clock and compass integers. For my purposes though, I mostly prefer working with the clock integers.

Note that the list above contains all constructible cyclotomic rings up to 24, and the next ones that follow after the digiclock integers should be the rings $\mathbb{Z}\mathbb{Z}_y$ with $y\in\{30,32,34\}$, because $30 = 2\cdot 3\cdot 5$, $32 = 2^5$ and $34 = 2\cdot 17$, here is an overview of valid parameters:

There are far more cyclotomic integers than you’d expect

Earlier, you have seen the Gaussian and Eisenstein integer lattices, and could naively, as I did, assume that all the rings will form a similar simple lattice as you have seen above. However, it turns out that once you go beyond the Eisenstein integers, you can reach many more different points in the same bounded area of the complex plane!

I wrote a little script that starts at the origin and explores the ring in a breadth-first-search inside the area of the complex plane bounded by the circle with radius 2 around the origin, up to some number of iterations. In each step, the current set of points is expanded by walking one unit into all directions possible in the ring. Thus, the color in the plots groups points that were discovered in the same round of the exploration.

Here are the Gaussian and Eisenstein integers that you have seen before:

As we saw before, both form a simple grid and in each finite area of the complex plane there are finitely many points that belong to that grid. Now for comparison, here are the plots for all the other rings in the list. You can easily identify the depicted ring based on the very apparent rotational symmetry that is emphasized by the colors:

Not only does the set of reachable points seem to never stop growing, but the pictures all exhibit a neat self-similar structure. The difference between Gaussian and Eisenstein integers and higher-order cyclotomic rings is that they are based on a field extension of the integers (or rationals) that is not simply a quadratic extension, because there are more linearly independent square roots. As a result, these extra “dimensions” result in this much richer structure when projected back into the 2D plane.

Note however that the rings are not dense in the plane, unless we would extend them to the rationals by closing them under division. But even with the limitation to rings, one can easily verify that we can find two elements in the ring with arbitrarily small distance (but not with arbitrarily small distance to any complex number, which would be required to be dense).

For the digiclock integers I reduced the number of exploration rounds, that is why that plot looks a bit different from the others (otherwise you could not see anything in the picture but a solid yellow circle). But what you can see instead is how the number of reachable points quickly explodes exponentially with the increasing number of different directions that are available.

Here are a few zoomed-in plots of the more tame (and also computationally efficient) clock integers. Note that the obviously missing points have just not been reached yet with the chosen number of rounds.

Tips for implementation of constructible cyclotomic rings

If you wonder how I found suitable symbolic roots to use, the answer is embarrassingly simple – a lot of guesswork and many hours of fooling around with Wolfram Alpha to transform and check complex number expressions, until I could see which common terms always show up and can be factored out. This was quite painful, given that there are myriads of equivalent ways how any given algebraic expression involving $i$ and various square roots can be written, but luckily it all worked out.

As I learned much later, you can make it more likely to give you the algebraic expressions you need by asking for $\cos(\frac{2\pi}{k})$ and $\sin(\frac{2\pi}{k})$ separately, and then putting this together to get an expression for $e^{\frac{2\pi i}{k}} = \cos(\frac{2\pi}{k}) + i\sin(\frac{2\pi}{k})$. Probably it knows about some relationships between cosines and square roots. Also, there apparently exists a systematic approach for deriving integral bases, but I did not try to make use of it.

I actually started without using Gaussian integers as coefficients, so for some of the rings I had to deal with $8\times 8$ matrices while understanding the multiplicative behavior of the symbolic dimensions. The repackaging to Gaussian integers reduced that down to just $4 \times 4$. So the definition of symbolic root numbers as presented above is actually the crystallized result out of a long and tedious process.

In general, if you have a set of square roots, you will need to carry around (a subset of) all products symbolically, as well. For example, you can see that if you have $\sqrt{2}$ and $\sqrt{3}$, you also need to take care of $\sqrt{2}\sqrt{3} = \sqrt{6}$, due to multiplication operations.

It is also crucial to recognize linear dependent square roots, for example:

• $\sqrt{2 + \sqrt{2}} = (\sqrt{2}+1)\sqrt{2 - \sqrt{2}}$
• $\sqrt{2 - \sqrt{2}} = (\sqrt{2}-1)\sqrt{2 + \sqrt{2}}$

Or similarly:

• $2\sqrt{2(5-\sqrt{5})} = (\sqrt{5}-1)\sqrt{2(5+\sqrt{5})}$
• $2\sqrt{2(5+\sqrt{5})} = (\sqrt{5}+1)\sqrt{2(5-\sqrt{5})}$

You may recognize these expressions from the table above. Out of such pairs, you have to pick only one to be part of your basis set, and if some algebra system combines both in expressions, you need to rewrite them accordingly to fit into the normal form with a fixed basis.

When you have a suitable set of roots, all that is left to do is tediously define a multiplication operation that correctly keeps track of the coefficients in terms of the chosen base. I did this by computing a symbolic multiplication matrix (luckily, that matrix is symmetric, halving the work) that can be seen as the outer product of all needed symbolic roots, then simplifying the resulting expressions, and finally summing the contributions for the same root over all matrix cells. This transparently resolves equivalences such as:

$$ x\sqrt{6} \cdot y\sqrt{15} = x\sqrt{2}\sqrt{3} \cdot y\sqrt{3}\sqrt{5} = 3xy\sqrt{2}\sqrt{5} = 3\cdot xy \cdot \sqrt{10} $$

More formally, for a given base of $n$ symbolic roots, for each pair of coefficient vectors $u=(u_{i})$ and $v=(v_{j})$ the multiplication tensor $M$ assigns to each $i,j,k \in \{1,…,n\}$ the contribution to the $k$-th symbolic root from the vector that represents the contribution of the multiplication of (the coefficients of) orthogonal symbolic roots $u_i$ and $v_j$. Thus, the result $w=(w_k)$ is given by $w_k := \sum_{i,j} M_{i,j,k} u_i v_j$. But I did not implement this conceptual tensor explicitly like that. Instead, to minimize the number of operations, I collected the resulting coefficients manually and simplified the added terms for each ring separately.

The parameters for which I built the rings were just some low hanging fruit I picked and succeeded with. For small parameters, this simple representation works well, but I am not sure if my symbolic complex root normal form would work for all of the possible rings – the expressions inside square roots can become rather complicated, involving increasingly nested roots that might cause difficulties. However, I never claimed that all these rings are representable that way, it is just a form I came up with that is very simple and convenient to work with.

Note that all the rings I presented here have an even number in the angle fraction $r$. I think that a factor of 2 is unavoidable due to the ability of negating a point, which is reflecting it to the opposite side across the origin, thereby “halving a unit rotation” if the underlying number of rotation steps is odd. For example, the Eisenstein integers can be defined by using only $\frac{1}{3}$ rotations, but you can still easily derive a $\frac{1}{6}$ unit length rotation (go and try it, it is very simple!), thus making them $\mathbb{Z}\mathbb{Z}_6$ in my classification.

In practice, it is convenient to work in rings with parameter that is multiple of 4, because then the imaginary unit $i$ itself is also part of the ring. Not having it can be cumbersome for certain applications, especially if you need to legally separate the real part from the imaginary.

All of this machinery can be easily generalized to work with $\mathbb{Q}$ by relaxing integrality of the coefficients (or equivalently, the requirement of a fixed scaling factor). The inverse of any number can be computed by rationalizing the denominator. This way you can extend the rings to fields, should you need this capability.

Using $\mathbb{Z}\mathbb{Z}_r$ to represent polygon vertex coordinates

In the beginning I claimed that all of this has something to do with 2D geometry and polygons. But I must admit that the whole framework of $\mathbb{Z}\mathbb{Z}_r$-based polygons I am working on is still a work-in-progress. What you have seen here is both an intermediate milestone in my project and an introduction preparing the stage for what comes next. There will definitely be a follow-up post, once it all has matured enough and as soon as time allows me to write it down. I just felt like this whole side-story about cyclotomic rings was big and interesting enough to stand on its own.

To give you a little glimpse, my unorthodox approach to polygons is based on describing them as a sequence of unit length steps in a sufficiently rich complex integer ring. Such an abstract sequence can be realized into a polygon boundary by following the respective directions from a chosen starting point and direction. It can be considered to be a kind of bare-bones Turtle graphics. Many common and interesting shapes can be described just by using this simple formalism, and it allows for some very efficient implementations of typically rather cumbersome operations^[3]. In the follow-up post, I am going to explain in detail how it all works, what the main limitations are, and what operations are supported.

I conclude this post with some pictures of shapes that you can draw even with the restriction to $\mathbb{Z}\mathbb{Z}_r$-valued vertex points. While it might not look very exciting or impressive, the key achievement here is that each vertex point is respresented internally only by integers^[4], there is no floating point arithmetic involved until the very last step of converting the numbers into screen or plot coordinates.

The top row shows the classic three regular polygons that tile the plane, the bottom row shows the two Penrose rhombus tiles, and finally the skeleton of the recently discovered spectre tile^[5]. The Penrose rhombs are represented using Penrose integers (obviously), all the others are based on clock integers.

In the follow-up post I will discuss how exactly paths of unit-length segments are used to describe polygonal tiles, what the advantage of this representation is, how to ensure that the resulting boundary is closed and not self-intersecting, and how compatible tiles can be combined to form larger tiles – and all that without the need of any fancy numerical computational geometry software or heavy algorithms, just by using this elegant algebraic approach.

Appendix: Some Python code

I talked so much about practical implementation of the rings that I cannot leave you without any code snippet for playing with these numbers. The implementation is certainly not optimal, but it works well enough for a proof-of-concept and was used to generate all the pictures (in combination with plotly).

Update (31.01.2024):
In this repo there is a Rust implementation of everything shown here, and more! However, you can still play with the simple and self-contained Python code below.

"""Naive implementation of complex integer rings in Python."""
# Copyright (C) 2024 Anton Pirogov, licensed under the MIT License
from __future__ import annotations

from typing import TypeVar, Generic, Type
from fractions import Fraction

from typing import Any
Self = Any

T = TypeVar("T")

class SymNum(Generic[T]):
    """Number from a complex integer ring with discrete rotation steps.

    This base class is just a wrapper around an integer, providing machinery for non-trivial subclasses.

    A number is represented as a vector of rational numbers,
    each component denoting the coefficient multiplied by a symbolic root term,
    such as i, sqrt(2), etc. (technically, we use it only for square roots
    of positive and negative integers).

    Note that there is no meaningful notion of a classical angle or distance between two
    points, because the result usually is not itself part of the ring or not uniquely
    defined inside the ring. Those values can be computed after conversion to the
    conventional complex numbers.

    See https://pirogov.de/blog/perfect-precision-2d-geometry-complex-integers/
    """
    NUM_TYPE: Type[T] = Fraction

    D_SQ: list[T] = [1]
    """Squares of units of the symbolic root dimensions that are represented by the number."""

    R: int = 1
    """Rotation unit in the ring is 1/R of a full turn."""

    L: int = 1
    """Dimension unit scaling factor is 1/L (needed to make all coefficients integers)."""

    _CCW: list[int] = [1]
    """Coefficients of normal form representation of the rotation unit."""

    # ----

    vec: list[T]
    """Vector with coefficients of the number."""

    @staticmethod
    def _mul(x: list[T], y: list[T]) -> list[T]:
        """Symbolic dimension multiplication table."""
        (a,), (b,) = x, y
        return [a * b]

    @classmethod
    def _ccw(cls) -> list[Fraction]:
        """Smallest unit rotation vector (generates all rotations)."""
        return list(map(lambda x: x * Fraction(1, cls.L), cls._CCW))

    def __init__(self, val: list[T] | int | Self[T] | None = None):
        if val is None:
            self.vec = [self.NUM_TYPE() for _ in range(len(self.D_SQ))]
        elif isinstance(val, SymNum):
            self.vec = list(val.vec)
        elif isinstance(val, int):
            one = self.NUM_TYPE(1) if not issubclass(self.NUM_TYPE, Fraction) else self.NUM_TYPE(1,1)
            self.vec = ([val*one] + [self.NUM_TYPE() for _ in range(len(self.D_SQ)-1)])
        else:
            assert len(val) == len(self.D_SQ)
            self.vec = list(val)

    @classmethod
    def zero(cls) -> Self:
        """Zero point."""
        return cls()

    @classmethod
    def one(cls) -> Self:
        """Unit pointing toward positive side of the real axis."""
        return cls(1)

    @classmethod
    def ccw(cls) -> Self:
        """Vector of smallest supported rotation."""
        return cls(cls._ccw())

    @classmethod
    def unit(cls, k: int = 0) -> Self:
        """Get a unit vector oriented into the desired direction."""
        return cls.one() * (cls.ccw()**k)

    # ----

    def __neg__(self) -> Self:
        return type(self)(list(map(lambda x: -x, self.vec)))

    def __add__(self, other: Self) -> Self:
        return type(self)(list(map(lambda a, b: a+b, self.vec, other.vec)))

    def __radd__(self, other: Self):
        return self + other 

    def __sub__(self, other: Self) -> Self:
        return self + (-other)

    def __mul__(self, other: int | Self) -> Self:
        if isinstance(other, int):
            # scalar multiplication
            return type(self)(list(map(lambda x: other*x, self.vec)))
        # special vector multiplication
        return type(self)(list(map(lambda x: x, self._mul(self.vec, other.vec))))

    def __rmul__(self, other):
        return self * other

    def __pow__(self, k: int) -> Self:
        if k < 0:
            k %= self.R
        result = type(self).one()
        for _ in range(k):
            result *= self
        return result


    def __iadd__(self, other: Self) -> Self:
        self.vec = (self+other).vec
        return self

    def __isub__(self, other: Self) -> Self:
        self.vec = (self-other).vec
        return self

    def __imul__(self, other: Self) -> Self:
        self.vec = (self*other).vec
        return self

    def __ipow__(self, k: int):
        self.vec = (self**k).vec
        return self

    # ----

    def __complex__(self) -> complex:
        """Convert to complex number, i.e. multiply and sum the encoded symbolic terms."""
        vec = self.vec
        if isinstance(vec[0], SymNum):
            vec = list(map(complex, self.vec))
        return sum(map(lambda c,d: c * complex(d)**(1/2), vec, self.D_SQ))

    def xy(self) -> tuple[float, float]:
        """Returns (Re(val), Im(val))."""
        c = complex(self)
        return (c.real, c.imag)

    def x(self) -> float:
        """Return Re(val)."""
        return self.xy()[0]

    def y(self) -> float:
        """Return Im(val)."""
        return self.xy()[1]

    # ----

    def __getitem__(self, ix):
        return self.vec[ix]

    def __iter__(self):
        return iter(self.vec)

    def __eq__(self, other) -> bool:
        for x, y in zip(self, other):
            if x != y:
                return False
        return True


    def __hash__(self) -> int:
        return hash(tuple(self.vec))


    def __bool__(self) -> bool:
        return any(map(bool, self.vec))


    def __repr__(self) -> str:
        return repr(self.vec).replace("array", type(self).__name__)

    def __str__(self) -> str:
        """Pretty-print number in human-readable algebraic form."""

        def fmt_d(d: int) -> str:
            if d == 1:
                return ""
            elif d == -1:
                return "1j"
            else:
                d_str = f"sqrt({abs(d)})"
                i_str ='1j*' if  d < 0 else ''
                return f"{i_str}{d_str}"

        def fmt_v(v) -> str:
            scaled = v * self.L
            if isinstance(v, (int, Fraction)):
                return str(int(scaled))
            else:
                tmp = str(scaled)
                return f"({tmp})" if "*" in tmp or "-" in tmp else tmp

        def fmt_term(v, d):
            v_str, d_str = fmt_v(v), fmt_d(d)
            if not d_str:
                return v_str
            if v_str == "1":
                return d_str
            return f"{v_str}*{d_str}"

        terms =[ fmt_term(v, d) for v, d in zip(self.vec, self.D_SQ) if v and d ]
        ret = "+".join(terms)

        if not ret:
            return "0"

        if "+" in ret:
            ret = f"({ret})"

        if self.L == 1:
            return ret
        return f"{ret}/{self.L}"


class GaussInt(SymNum):
    """Numbers with 90 degree rotations (Gaussian integers).

    This is the only instance where the resulting dimensions are orthogonal
    and exactly match the two axes of the complex plane.
    """
    R = 4
    D_SQ = [1, -1]
    L = 1
    _CCW = [0, 1]

    @staticmethod
    def _mul(x, y):
        (a, b), (c, d) = x, y
        return [
            a*c - b*d,
            a*d + b*c
        ]

class EisensteinInt(SymNum):
    """Numbers with 60 degree rotations (Eisenstein).

    Note that this is equivalent to using 120 degree rotations as basis, but
    the 120 degree rotation basis is improper, because it is not minimal
    (one can produce 60 deg. rotations from linear combinations of 120 degree rotations).

    Can also be represented in symbolic root normal form (see EisenClockInt).
    """
    R = 6
    D_SQ = [1, -3]
    L = 2
    _CCW = [1, 1]

    @staticmethod
    def _mul(x, y):
        (a, b), (c, d) = x, y
        return [
            a*c - 3*b*d,
            a*d +   b*c
        ]


class CSymNum(SymNum[GaussInt]):
    """A complex symbolic root number with Gaussian Integers as coefficients.

    This base class is just a wrapper around a GaussInt, providing machinery
    to represent different complex integer rings in symbolic root normal form, i.e

    1/l(c_i*sqrt(d_i)) with c_i being Gaussian integers, l in Z, d_i in R+.
    """
    NUM_TYPE = GaussInt
    _CCW = [(0, 1)]

    @classmethod
    def _ccw(cls) -> list[Fraction]:
        def to_sym(xy: tuple[int, int]):
            x, y = xy
            return cls.NUM_TYPE([Fraction(x, cls.L), Fraction(y, cls.L)])

        return list(map(to_sym, cls._CCW))



class CompassInt(CSymNum):
    """Numbers with 45 degree rotations (compass integers)."""
    R = 8
    D_SQ = [1, 2]
    L = 2
    _CCW = [(0,0), (1,1)]

    @staticmethod
    def _mul(x, y):
        # Dimension multiplication matrix (for Z[i]-valued vectors):
        #    c d
        # a [1 s]
        # b [s 2]
        # where s = sqrt(2)
        (a, b), (c, d) = x, y
        return [
            a*c + 2*b*d,
            a*d +   b*c,
        ]


class PenroseInt(CSymNum):
    """Numbers with 36 degree rotations (Penrose integers)."""
    PENTA = 2*(5-5**(1/2))  # common term for needed symbolic root dimensions

    R = 10
    D_SQ = [1, 5, PENTA, 5*PENTA]
    L = 8
    _CCW = [(2,0), (2,0), (0,2), (0,0)]

    # condensed version (if vectors were Z[i]-valued):
    # x=sq5, y=2(5-x)
    #    e     f      g        h
    # a [1   ,  x   ,   y    ,   xy   ]
    # b [ x  , 5    ,  xy    ,  5 y   ]
    # c [  y ,  xy  , 10-2x  , 10(x-1)]
    # d [ xy , 5 y  , 10(x-1), 10(5-x)]
    # where x = sqrt(5), y = sqrt(2*(5-sqrt(5)))
    @staticmethod
    def _mul(x, y):
        (a, b, c, d), (e, f, g, h) = x, y
        return [
            a*e + 5*b*f + 10*(c*g + 5*d*h - c*h - d*g),
            a*f + b*e - 2*c*g + 10*(c*h + d*g - d*h),
            a*g + 5*(b*h + d*f) + c*e,
            a*h + b*g + c*f + d*e,
        ]


class ClockInt(CSymNum):
    """Numbers with 30 degree rotations (clock integers)"""
    R = 12
    D_SQ = [1, 3]
    L = 2
    _CCW = [(0, 1),(1, 0)]

    @staticmethod
    def _mul(x, y):
        # Dimension multiplication matrix (for Z[i]-valued vectors):
        #    c d
        # a [1 s]
        # b [s 3]
        # where s = sqrt(3)
        (a, b), (c, d) = x, y
        return [
            a*c + 3*b*d,
            a*d +   b*c,
        ]


class EisenClockInt(ClockInt):
    """Normal-form representation of Eisenstein numbers (just for illustration purposes)."""
    R = 6

    @classmethod
    def _ccw(cls):
        return (ClockInt.ccw()**2).vec


class DigiClockInt(CSymNum):
    """Numbers with 15 degree rotations (digiclock numbers)."""
    R = 24
    D_SQ = [1, 2, 3, 6]
    L = 4
    _CCW = [(0,0), (1, -1), (0,0), (1,1)]

    @staticmethod
    def _mul(x, y):
        # Dimension multiplication matrix (for Z[i]-valued vectors):
        #     e    f     g    h
        # a [1   ,  x  ,   y ,  xy ]
        # b [ x  , 2   ,  xy , 2 y ]
        # c [  y ,  xy , 3   , 3x  ]
        # d [ xy , 2 y , 3x  , 6   ]
        (a, b, c, d), (e, f, g, h) = (x, y)
        return [
            a*e + 2*b*f + 3*c*g + 6*d*h,
            a*f + b*e + 3*(c*h + d*g),
            a*g + c*e + 2*(b*h + d*f),
            a*h + b*g + c*f + d*e,
        ]

ZZ = {
    4: GaussInt,
    6: EisensteinInt,
    8: CompassInt,
    10: PenroseInt,
    12: ClockInt,
    24: DigiClockInt,
}
"""Convenience access to different complex integer classes."""


def test_rings():
    from math import e, pi

    for cl in ZZ.values():
        print("Testing units of ring", cl.__name__, f"= ZZ_{cl.R}")

        # half cycle = -1
        assert cl.unit(cl.R//2) == -cl.one()
        assert complex(-cl.one()) == -1

        # full cycle = 1
        assert cl.unit(cl.R) == cl.one()
        assert complex(cl.one()) == 1

        # check deviation from reference of complex rotation vs matrix
        # and correctness of direct multiplication table vs rotation matrix
        for k in range(-cl.R, cl.R + 1):
            ref = e**(2j*pi*k/cl.R)
            unit = cl.unit(k)
            assert abs(complex(unit)-ref) < 1e-15

        # check unit multiplication (should rotate correctly)
        for m in range(-cl.R, cl.R + 1):
            for n in range(-cl.R, cl.R + 1):
                mul_result = cl.unit(m) * cl.unit(n)
                exp_add_result = cl.unit(m + n)
                assert mul_result == exp_add_result

A little demonstration:

>>> from math import sqrt
>>> print(*map(lambda x: f"{x} = {eval(str(x))}", (ZZ[12].unit(i) for i in range(ZZ[12].R))), sep="\n")
2/2 = 1.0
(1j+sqrt(3))/2 = (0.8660254037844386+0.5j)
(1+1j*sqrt(3))/2 = (0.5+0.8660254037844386j)
(2*1j)/2 = 1j
((-1)+1j*sqrt(3))/2 = (-0.5+0.8660254037844386j)
(1j+(-1)*sqrt(3))/2 = (-0.8660254037844386+0.5j)
(-2)/2 = -1.0
((-1*1j)+(-1)*sqrt(3))/2 = (-0.8660254037844386-0.5j)
((-1)+(-1*1j)*sqrt(3))/2 = (-0.5-0.8660254037844386j)
(-2*1j)/2 = (-0-1j)
(1+(-1*1j)*sqrt(3))/2 = (0.5-0.8660254037844386j)
((-1*1j)+sqrt(3))/2 = (0.8660254037844386-0.5j)

>>> point = ZZ[12].unit(0) + 2*ZZ[12].unit(1)
>>> point
[[Fraction(1, 1), Fraction(1, 1)], [Fraction(1, 1), Fraction(0, 1)]]

>>> complex(point)  # == 1+2*e**(1j*pi/6)
(2.732050807568877+1j)

1. Notice how the geometrical interpretation of polar coordinates naturally implies and maps onto these actions. ↩

2. These were also the most painful to figure out, and the reason why in the definition above I had to allow $d_i \in \mathbb{R}_+$ instead of $\mathbb{N}$. Note that the Halfrose integers are very similar, but impractical, as they do not allow to have a quarter turn and thus represent the imaginary unit. ↩

3. However, I cannot fully exclude the possibility that I am in the process of reinventing the wheel, as often. Maybe the tricks I found are already folk wisdom and old news, but who knows. ↩

4. If you would see the code, you’d notice that the coordinates are implemented as rational numbers, because I did not figure out a nice way to pull out the $\frac{1}{l}$ factors out of my matrices without everything becoming a big mess. But as a rational numbers are pairs of integers, this is just a nitpicky technical detail. ↩

5. Technically, this is an instance of the hat tile, the spectre is obtained from this polygon by replacing all the segments connecting vertices with certain curves. You can even get your own set of spectres as a wooden puzzle! That was one impulse buy I did not regret at all. ↩