Designing the Advaya and Atreya Tile Sets

In this article I explain the motivation, reasoning and decisions that resulted in the tile sets that are used for my games Advaya and Atreya.

In the beginning there was an aesthetic desire – I wanted a game somewhat like Carcassone, but with hexagonal instead of square tiles, and without any chance involved. Some people already thought about hexagonal Carcassonne and it seems that the mechanics of the game would not work as well as with square tiles, because it is more difficult to find tiles that match exactly into constrained gaps with many neighbors. So I decided that instead of trying to retrofit a game I like onto a shape I like, it was the time for me to create a completely new game.

I also enjoy Hive and am fascinated by the whole idea that the movable pieces are also the game board itself, so I wanted to create a game that combines the main mechanics of both games in a sensible way. I quickly decided that the game should be a minimalistic and portable one and that I would prefer to have no other items except for the hexagonal tiles themselves.

Unlike Carcassonne, abstracts like Hive have a timeless elegance to them that I would also strive for. To have this kind of quality, I did not want to come up with a random set of tiles that does the job, I wanted the tile set to be a complete set of tiles that satisfy some reasonable constraints, to make the theoretician in me happy. I wanted to have a tile set which in some sense is dual to Serpentiles, i.e. instead of playing paths you play areas.

Setting up the constraints

As there are zillions of possibilities for different hexagonal tiles that behave sort-of like Carcassonne tiles, i.e. are colored with area types (in Carcassonne: Grass, Road, City), the first restriction that I decided to introduce was to only consider tiles with planar connectivity, i.e. you can not have a connection over or under another connection (in Carcassonne some tiles do that, e.g. two cities connected by a bridge over a road). This eliminates many of the possible connectivity types that a tile can have.

Next, I had to decide on the allowed types of boundary that is added to the tile to separate the planar areas from each other. To keep things simple, I decided that I will only consider tiles that can be drawn onto a hexagon by placing line segments that start and end in either a corner or the center of the hexagon, so that the drawn inner segments and the hexagon boundary edges separate the hexagon into multiple proper polygons (i.e., no dangling line segment to the center).

I also thought about allowing semicircles or flatter triangles to be used as a boundary between adjacent corners. This seems at first like an attractive option that allows some connectivity variants (mostly, some more tunnel-style tiles) that are not possible when only using little triangle pieces that must touch the center. For semicircles, doing this requires the introduction of more constraints concerning other line segments that touch these semicircles to avoid problematic intersections, and even after taking care of that, it turned out that shapes containing such semicircles just look weird. Equivalent tiles can be obtained when allowing flatter triangles, but this variant introduces too many possibilities, which would give me another reason to add new restrictions to prevent ugly or redundant tiles. Sometimes less is more and as the tile set appears to be better off without such tiles, I discarded both possibilities at the cost of sacrificing a handful of tiles that I would like to have in the set, but see no way of adding without also adding many tiles I would rather exclude.

Finding all different tile types, and more constraints

I generated the tiles by first numbering the corners $0-5$, starting on the right and going counterclockwise, and then called the center $6$ (making the center $6$ instead of $0$ simplifies the calculation of e.g. rotations). Each permissible segment is just a pair of different numbers between $0$ and $6$, so that it suffices to provide a list of segments to describe a tile (in the image below, tile type 5 is described by the segments $(0,2),(1,3)$). Now there can be multiple descriptions that lead to the same resulting tile. To fix that, I only allow the shortest representation, i.e. instead of describing a line through the center using segments $(0,6)$ and $(3,6)$ you have to use the segment $(0,3)$. Furthermore, I always write segments with the smaller number first and in lexicographic order, so e.g. $(0,6)$ comes before $(1,3)$. Finally, to get rid of rotationally equivalent tiles, I rotate the coordinates in all 6 possible ways and normalize it again. Of those possibilities I keep the lexicographically smallest sequence, i.e. ${(0,3),(1,6)}$ instead of ${(1,4),(2,6)}$.

Implementing this is a tedious but simple exercise that tells us that there are in fact 337 tile types satisfying the constraints I introduced so far, but this includes many tiles that have areas that are completely enclosed by other areas on the tile. For rather obvious reasons such tiles are not interesting for an edge-matching game, so such tiles are also excluded. This restriction essentially kicks out all tiles that have more than 6 areas, because each area needs at least one hex boundary edge. This is good, because so many areas on a single tile is too much structure for a single game piece anyway. As a side effect, some other unfortunate combinations with at most 6 areas are also removed. This leaves us with only 62 tile types left to work with, which is still a lot, but a managable number for human inspection:

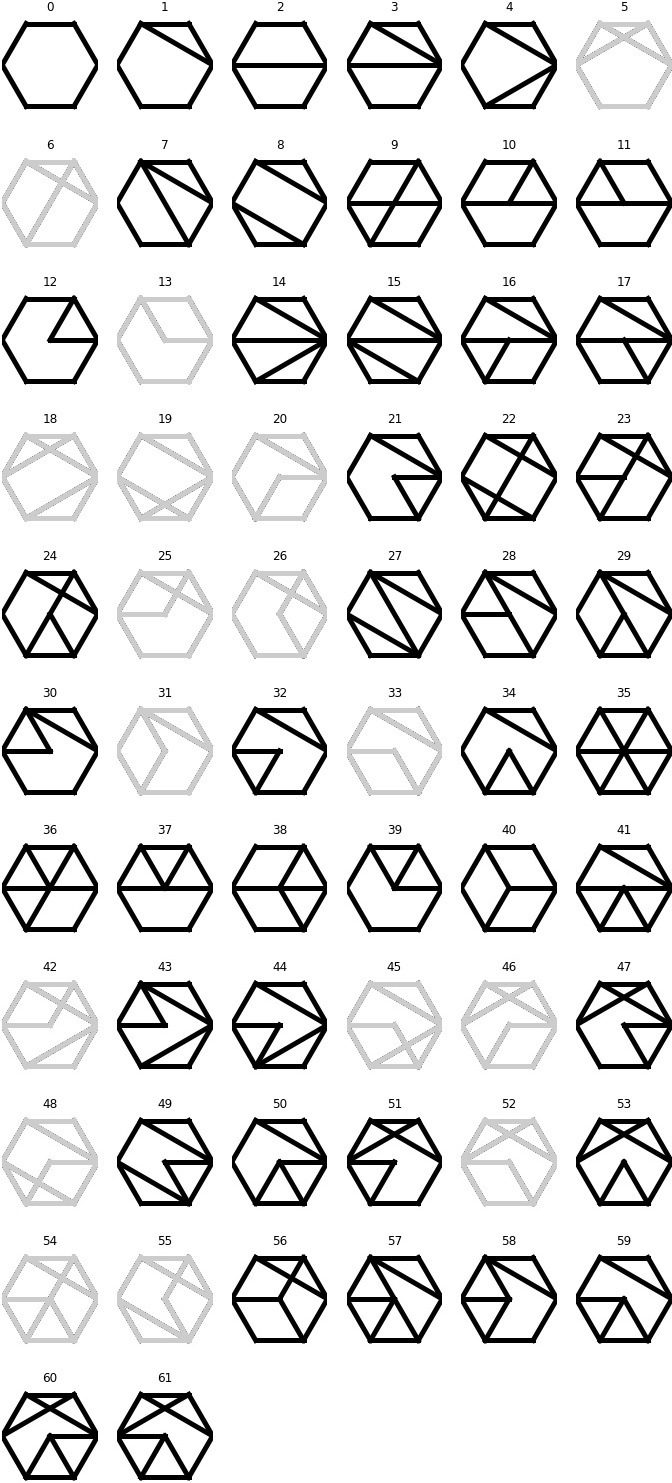
Notice that some tile types are reflections of other types (like 3 and 7) and furthermore there are still topologically equivalent tile types that just look different, so they have the same connectivity properties both inside the tile and to the outside (like 5 and 37). I removed equivalent types by hand (those are greyed out) and always kept the ones I liked more. I preferred the tiles where lines only intersect in the center (if at all) where this is possible, instead of at other points. Apart from this, all else being equal I kept the tiles that can be drawn with fewer line segments or that are more symmetric (I think this roughly covers all my decisions). I hope I did not mess up this step, but doing it by hand is faster then programming it. As the result there remain 45 useful tile types.

From tile types to a tile set

The original plan was to create tiles with three colors. I quickly had envisioned essentially a more complex variant of Advaya with three colors for 2-3 players, where in the 3-player variant the colors dominate each other in a rock-paper-scissors manner, while the 2-player version was almost Advaya, with an additional neutral color. But I was still struggling with the definition of a satisfying tile set. The problem is that there still remain too many tile types for considering a complete set that contains every possible coloring of the areas.

I played with various additional restrictions, like permitting only tiles where all areas are convex polygons, or restricting the number of polygons per tile. I also thought about making the hexagons flippable, to merge types that are reflections of each other. One difficulty is that the more different pieces there are on a tile, the more different colorings are possible. While there are already many similar-looking tile types with 4 or 5 areas, they also produce the greatest number of colorings (some tile types admit up to 36 different colorings!), leading to an unbalanced and rather boring set of tiles. Having a tile set where most tiles look similar defeats the whole purpose of this project. I don’t know whether this would actually be a big problem in practice, but it is not very satisfying. The sets I came up with still had about 120-140 tiles of about 15-18 remaining different tile types and none of them really felt just right yet.

Finally I gave up on the three colors and tried to modify the game for two colors and two players. Removing the third color is a drastic step — it immediately removes all tile types where the connectivity graph of the areas is not bipartite, or equivalently, where this graph has cycles of odd length. Furthermore, for those types that remain there are only the two obvious colorings possible (that can still result in the same tile). While initially I have always excluded tiles with non-convex polygons, now I decided to include them, because the tile set even seemed to be too small without and I could get rid of this arbitrary restriction. The last step was to exclude the blank monocolored tile type, because it somehow does not fit in with the spirit of the rest. The result are the Advaya tiles. The names of the tiles mostly correspond to the letters or symbols that the lines resemble, with some added alignment information to separate similar tiles.

To wrap it up, the 49 Advaya tiles are all the different colorings (I,*,H,S,N are unique, the rest is paired) of all the 27 hex tile types that satisfy the following reasonable properties:

1. Tiles are described by maximal line segments that start and end in corners or the center.

2. Each tile contains at least one boundary line segment, i.e. at least two polygons.

3. Each area shares an edge with the hexagon, i.e. there are no closed shapes on a tile.

4. The connectivity graph of the tile is 2-colorable.

5. There is at most one tile type (and its reflection) for each inner+outer connectivity type.

I am quite happy with this 2-colored tile set and enjoy playing Advaya. First ideas for rules of the game emerged even before the tile set was complete and the current rules are a pragmatic compromise that I believe is also fun to play without computer support.

From Advaya to Atreya

Some time after temporarily giving up on the three-color version, I was just toying around with geometry and graphics without any specific purpose in mind. Starting with hexagon corners as your initial set of points, connect each pair of them with a line segment and add all intersection points to your set. Now what happens when you iterate this process to the limit? This very quickly becomes computationally infeasible, but what is generated after the second iteration is the decorative part you can see in the Atreya logo:

After looking at this for a while, I noticed the smaller hexagon that emerged on the inside, which has exactly half the width of the outer hexagon. Almost immediately it was also clear, that this central inner hexagon is surrounded by semi-hexagons on all its six sides. This shape deviates from the Advaya tile shapes and has a completely different aesthetic, but it was apparent that it harbors interesting possibilities (including a three-way tunnel, which I’d like to have) and results in a nice regular honeycomb pattern, so I just gave it a try. Starting from this shape, it was obvious what to do—I generated all possible distinct three-colorings of the 7 pieces that the tile consists of. The tile boundaries were implicitly derived by adding them between pieces of different color. In the spirit of Advaya, where all tiles feature both colors, I restricted the set to colorings where all three colors must appear on some semi-hexagon of the boundary, which also automatically ensures that the central hexagon is not an isolated closed shape.

The result were 273 different tiles, which still seemed like too much. So I used the same idea I already have tried before and just placed all reflected versions on the backsides of the tiles, which yields the 168 tiles. This set is still a bit larger than what I intended, but to reduce this number even further, I would have needed to introduce unnatural restrictions, so I decided to leave it as is:

Even though the resulting tiles are very regular and seem to be so simple that there must already exist a game using these tiles, I am not aware of any such games and this tile set is obviously complete, does not use constraints that feel wrong and because all tiles have the same shape anyway, there is no imbalance in the proportion of tiles with different shapes that was annoying me in the case of the Advaya tile shapes. So here it is, the surprisingly simple solution I arrived at.

I decided to give the game variant using these tiles a different name, because the tiles are so different and the rules require some adaptations—while some Advaya mechanisms do not work anymore (backsides are not opposite tiles anymore), new possibilities arise due to the third color. I think the result is interesting on its own and feels quite different from Advaya, even though it is almost the same game.

While I really like the Advaya tile set for its very unique look and it seems more fun for building areas that look like abstract art, I think that the Atreya tile set has more potential to be used for different kinds of games, especially games where additional game pieces are placed on top of the tiles. Probably I will explore the possibilities further, after being completely satisfied with Advaya/Atreya.

Connectivity and progress

When playing Advaya according to the rules (bi-connected, without holes), one can show that the arena will always have at least one position where a tile needs to match at most 3 successive colors (and more than 4 is never necessary for valid moves, because a tile can not slide in such a narrow gap), so an interesting question is whether it is always possible to play a tile from the pool validly.

There are 4 categories of tiles—18 tiles have both a singleton piece and some combination of pieces such that 3 successive borders have the same color. This together with their dual backsides is enough to be able to match the tile to a location with at most three successive borders to match, for any of the 8 possible colorings. On the other extreme, there are 4 tiles that have only singleton pieces and those are probably the hardest to match in constrained positions. The third group of 11 tiles consists of tiles with 2-4 or 3-3 borders that lack singleton pieces, so cannot match black-white-black or white-black-white, and the fourth group with 16 tiles has the opposite problem of lacking a monocolored border of length 3, so these cannot match black-black-black or white-white-white.

In practice, I think it is very unlikely to reach a position where no tile can be played from the pool and it took me some time to construct such a situation artificially:

I suppose that there is also a situation where all tiles are in the arena, all but at least two (we need two because the players may not move the same tile in consecutive moves) are pinned, whereas those can be moved around, but never pinned, making progress impossible even though there are always allowed moves. This edge case would be interesting because it does not lead to game termination, but to a unproductive infinite loop. Unfortunately I have not managed to construct such an arena yet, but also have no proof that this is impossible. Furthermore, even if it is impossible, it might be not immediately clear how to move the tiles around so that the game terminates.

Anyway, I think that those and other artificial special cases will basically never occur in a real game. If chess was fully understood before playing it, then well, still nobody would play it except for researchers and obviously these questions do not matter too much in practice. For all practical purposes, this matter is resolved by the stagnation rule, which is a crutch, but a necessary one, because I see no natural stopping point for the game.

I have not analyzed the Atreya tiles in that much detail like Advaya, but it seems that the connectivity possibilities there are non-surprisingly more restricted. A single tile can not cover all the possible 3-gaps like it is the case with Advaya. Notice that we have no dual coloring on the backside, just the reflection (it still helps, but not too much), and even with backsides we can cover at most 12 out of $3^3=27$ possibilities. I am still quite optimistic that one will not run into problems with finding a matching and useful tile in Atreya too often.